NCERT Solutions | Class 12 Maths Chapter 10

NCERT Solutions | Class 12 Maths Chapter 10 | Vector Algebra 

CBSE Solutions | Maths Class 12

Check the below NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Pdf free download. NCERT Solutions Class 12 Maths  were prepared based on the latest exam pattern. We have Provided Vector Algebra Class 12 Maths NCERT Solutions to help students understand the concept very well.

NCERT | Class 12 Maths

NCERT Solutions Class 12 Maths

Book:	National Council of Educational Research and Training (NCERT)
Board:	Central Board of Secondary Education (CBSE)
Class:	12th
Subject:	Maths
Chapter:	10
Chapters Name:	Vector Algebra
Medium:	English

Vector Algebra | Class 12 Maths | NCERT Books Solutions

You can refer to MCQ Questions for Class 12 Maths Chapter 10 Vector Algebra to revise the concepts in the syllabus effectively and improve your chances of securing high marks in your board exams.

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.1

Ex 10.1 Class 12 Maths Question 1.

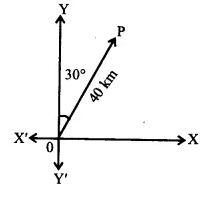
Represent graphically a displacement of 40km, 30° east of north.
Solution.
A line segment of 2 cm is drawn on the right of OY making an angle of 30° with it. OP = 40 km,
scale 1cm = 20 km. Vector \(\overrightarrow { OP } \) represents displacement of 40 km 30° east of north.

Ex 10.1 Class 12 Maths Question 2.
Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 metres north- west
(iii) 40°
(iv) 40 watt
(v) 10^-19 coulomb
(vi) 20 m/sec².
Solution.
(i) Mass-scalar
(ii) Directed distance-vector
(iii) Temperature-scalar
(iv) Rate of electricity-scalar
(v) Electric charge-vector
(vi) Acceleration-vector

Ex 10.1 Class 12 Maths Question 3.
Classify the following as scalar and vector quantities
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v)work.
Solution.
Scalar Quantity: (i) time period (ii) distance (v) work.
Vector Quantity: (iii) force (iv) velocity

Ex 10.1 Class 12 Maths Question 4.
In a square, identify the following vectors
(i) Co-initial
(ii) Equal
(iii) collinear but not equal
Solution.
(i) Co initial vectors are \(\overrightarrow { a } ,\overrightarrow { d } \)
(ii) Equal Vectors are \(\overrightarrow { b } ,\overrightarrow { d } \)
(iii) Collinear but not equal vectors are \(\overrightarrow { a } ,\overrightarrow { c } \)

Ex 10.1 Class 12 Maths Question 5.
Answer the following as true or false:
(i) \(\overrightarrow { a } ,\overrightarrow { -a } \) are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Solution.
(i) True
(ii) False
(iii) False
(iv) False.

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.2

Ex 10.2 Class 12 Maths Question 1.
Compute the magnitude of the following vectors:
\(\overrightarrow { a } =\hat { i } +\hat { j } +\hat { k } ,\overrightarrow { b } =\hat { 2i } -\hat { 7j } -\hat { 3k } \)
\(\overrightarrow { c } =\frac { 1 }{ \sqrt { 3 } } \hat { i } +\frac { 1 }{ \sqrt { 3 } } \hat { j } -\frac { 1 }{ \sqrt { 3 } } \hat { k } \)
Solution.
\(\overrightarrow { a } =\hat { i } +\hat { j } +\hat { k } \)
\(\left| \overrightarrow { a } \right| =\sqrt { { 1 }^{ 2 }+{ 1 }^{ 2 }+{ 1 }^{ 2 } } \)

<

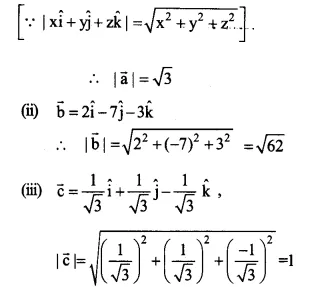
Ex 10.2 Class 12 Maths Question 2.
Write two different vectors having same magnitude.
Solution.
\(\overrightarrow { a } =\hat { i } +\hat { 2j } +\hat { 3k } ,\overrightarrow { b } =\hat { 3i } +\hat { 2j } +\hat { k } \)

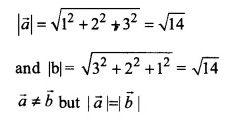
Such possible answers are infinite

Ex 10.2 Class 12 Maths Question 3.
Write two different vectors having same direction.
Solution.
Let the two vectors be
\(\overrightarrow { a } =\hat { i } +\hat { j } +\hat { k } ,\overrightarrow { b } =\hat { 3i } +\hat { 3j } +\hat { 3k } \)

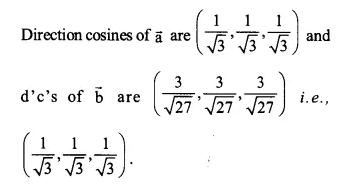
Hence vectors \(\overrightarrow { a } ,\overrightarrow { b } \) have the same direction but different magnitude

Ex 10.2 Class 12 Maths Question 4.
Find the values of x and y so that the vectors \(\overrightarrow { 2i } +\overrightarrow { 3j } \quad and\quad \hat { xi } +\hat { yj } \) are equal.
Solution.
We are given \(\overrightarrow { 2i } +\overrightarrow { 3j } \quad and\quad \hat { xi } +\hat { yj } \)
If vectors are equal, then their respective components are equal. Hence x = 2, y = 3.

Ex 10.2 Class 12 Maths Question 5.
Find the scalar and vector components of the vector with initial point (2,1) and terminal point (-5,7).
Solution.
LetA(2, 1) be the initial point and B(-5,7) be the terminal point \(\overrightarrow { AB } =\left( { x }_{ 2 }-{ x }_{ 1 } \right) \hat { i } +\left( { y }_{ 2 }-{ y }_{ 1 } \right) \hat { j } =-\hat { 7i } +\hat { 6j } \)
∴The vector components are \(-\hat { 7i } and\hat { 6j } \) and scalar components are – 7 and 6.

Ex 10.2 Class 12 Maths Question 6.
Find the sum of three vectors:
\(\overrightarrow { a } =\hat { i } -\hat { 2j } +\hat { k } ,\overrightarrow { b } =-2\hat { i } +\hat { 4j } +5\hat { k } \quad and\quad \overrightarrow { c } =\hat { i } -\hat { 6j } -\hat { 7k } ,\)
Solution.
\(\overrightarrow { a } =\hat { i } -\hat { 2j } +\hat { k } ,\overrightarrow { b } =-2\hat { i } +\hat { 4j } +5\hat { k } \quad and\quad \overrightarrow { c } =\hat { i } -\hat { 6j } -\hat { 7k } ,\)
\(\overrightarrow { a } +\overrightarrow { b } +\overrightarrow { c } =\hat { 0i } -\hat { 4j } -\hat { k } =-4\hat { i } -\hat { k } \)

Ex 10.2 Class 12 Maths Question 7.
Find the unit vector in the direction of the vector
\(\overrightarrow { a } =\hat { i } +\hat { j } +\hat { 2k } \)
Solution.
\(\overrightarrow { a } =\hat { i } +\hat { j } +\hat { 2k } \)

Ex 10.2 Class 12 Maths Question 8.
Find the unit vector in the direction of vector \(\overrightarrow { PQ } \), where P and Q are the points (1,2,3) and (4,5,6) respectively.
Solution.
The points P and Q are (1, 2, 3) and (4, 5, 6) respectively
\(\overrightarrow { PQ } =(4-1)\hat { i } +(5-2)\hat { j } +(6-3)\hat { k } \)

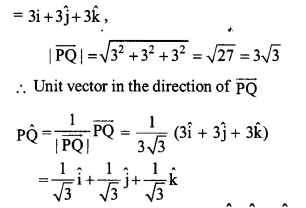
Ex 10.2 Class 12 Maths Question 9.
For given vectors \(\overrightarrow { a } =2\hat { i } -\hat { j } +2\hat { k } \quad and\quad \overrightarrow { b } =-\hat { i } +\hat { j } -\hat { k } \) find the unit vector in the direction of the vector \(\overrightarrow { a } +\overrightarrow { b } \)
Solution.
\(\overrightarrow { a } =2\hat { i } -\hat { j } +2\hat { k } \quad and\quad \overrightarrow { b } =-\hat { i } +\hat { j } -\hat { k } \)

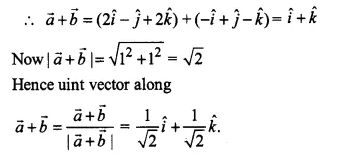
Ex 10.2 Class 12 Maths Question 10.
Find a vector in the direction of \(5\hat { i } -\hat { j } +2\hat { k } \) which has magnitude 8 units.
Solution.
The given vector is \(\overrightarrow { a } =5\hat { i } -\hat { j } +2\hat { k } \)

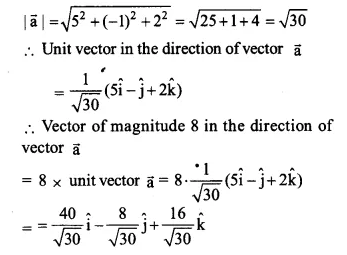
Ex 10.2 Class 12 Maths Question 11.
Show that the vector \(2\hat { i } -3\hat { j } +4\hat { k } \quad and\quad -4\hat { i } +6\hat { j } -8\hat { k } \) are collinear.
Solution.
\(\overrightarrow { a } =2\hat { i } -3\hat { j } +4\hat { k } \quad and\quad \overrightarrow { b } =-4\hat { i } +6\hat { j } -8\hat { k } \)
\(=-2(2\hat { i } -3\hat { j } +4\hat { k } ) \)
vector \(\overrightarrow { a } \quad and\quad \overrightarrow { b } \) have the same direction they are collinear.

Ex 10.2 Class 12 Maths Question 12.
Find the direction cosines of the vector \(\hat { i } +2\hat { j } +3\hat { k } \)
Solution.
let \(\overrightarrow { p } =\hat { i } +2\hat { j } +3\hat { k } \)
Now a = 1,b = 2,c = 3

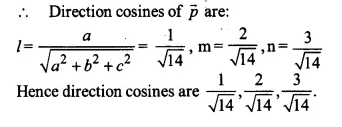
Ex 10.2 Class 12 Maths Question 13.
Find the direction cosines of the vector joining the points A (1,2, -3) and B(-1, -2,1), directed fromAtoB.
Solution.
Vector joining the points A and B is
\(({ x }_{ 2 }-{ x }_{ 1 })\hat { i } +({ y }_{ 2 }-{ y }_{ 1 })\hat { j } +({ z }_{ 2 }-{ z }_{ 1 })\hat { k } \)

Ex 10.2 Class 12 Maths Question 14.
Show that the vector \(\hat { i } +\hat { j } +\hat { k } \) are equally inclined to the axes OX, OY, OZ.
Solution.
Let \(\hat { i } +\hat { j } +\hat { k } =\overrightarrow { a } \) , Direction cosines of vector \(x\hat { i } +y\hat { j } +z\hat { k } \) are

which shows that the vector a is equally inclined to the axes OX, OY, OZ.

Ex 10.2 Class 12 Maths Question 15.
Find the position vector of a point R which divides the line joining the points whose positive vector are \(P(\hat { i } +2\hat { j } -\hat { k } )\quad and\quad Q(-\hat { i } +\hat { j } +\hat { k } )\) in the ratio 2:1
(i) internally
(ii) externally.
Solution.
(i) The point R which divides the line joining the point \(P(\overrightarrow { a } )\quad and\quad Q(\overrightarrow { b } )\) in the ratio m : n

Ex 10.2 Class 12 Maths Question 16.
Find position vector of the mid point of the vector joining the points P (2,3,4) and Q (4,1, -2).
Solution.
Let \(\overrightarrow { OP } =2\hat { i } +3\hat { j } +4\hat { k } \quad and\quad \overrightarrow { OQ } =4\hat { i } +\hat { j } -2\hat { k } \)

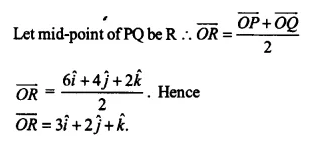
Ex 10.2 Class 12 Maths Question 17.
Show that the points A, B and C with position vector \(\overrightarrow { a } =3\hat { i } -4\hat { j } -4\hat { k } ,\overrightarrow { b } =2\hat { i } -\hat { j } +\hat { k } and\quad \overrightarrow { c } =\hat { i } -3\hat { j } -5\hat { k } \) respectively form the vertices of a right angled triangle.
Solution.
\(\overrightarrow { AB } =\overrightarrow { b } -\overrightarrow { a } =-\hat { i } +3\hat { j } +5\hat { k } \)

Ex 10.2 Class 12 Maths Question 18.
In triangle ABC (fig.), which of the following is not

(a) \(\overrightarrow { AB } +\overrightarrow { BC } +\overrightarrow { CA } =\overrightarrow { 0 } \)
(b) \(\overrightarrow { AB } +\overrightarrow { BC } -\overrightarrow { AC } =\overrightarrow { 0 } \)
(c) \(\overrightarrow { AB } +\overrightarrow { BC } -\overrightarrow { CA } =\overrightarrow { 0 } \)
(d) \(\overrightarrow { AB } -\overrightarrow { CB } +\overrightarrow { CA } =\overrightarrow { 0 } \)
Solution.
We know that
\(\overrightarrow { AB } +\overrightarrow { BC } +\overrightarrow { CA } =\overrightarrow { 0 } \)
\(\overrightarrow { AB } +\overrightarrow { BC } -\overrightarrow { AC } =\overrightarrow { 0 } \)
Hence option (c) is not correct

Ex 10.2 Class 12 Maths Question 19.
If \(\overrightarrow { a } ,\overrightarrow { b } \) are two collinear vectors then which of the following are incorrect:
(a) \(\overrightarrow { b } =\lambda \overrightarrow { a } \), for some scalar λ.
(b) \(\overrightarrow { a } =\pm \overrightarrow { b } \)
(c) the respective components of \(\overrightarrow { a } ,\overrightarrow { b } \) are proportional.
(d) both the vectors \(\overrightarrow { a } ,\overrightarrow { b } \) have same direction, but different magnitudes.
Solution.
Options (d) is incorrect since both the vectors \(\overrightarrow { a } ,\overrightarrow { b } \) , being collinear, are not necessarily in the same direction. They may have opposite directions. Their magnitudes may be different.

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.3

Ex 10.3 Class 12 Maths Question 1.
Find the angle between two vectors \(\overrightarrow { a } ,\overrightarrow { b } \) with magnitudes √3 and 2 respectively, and such that \(\overrightarrow { a } \cdot \overrightarrow { b } =\sqrt { 6 } \)
Solution.
Angle θ between two vectors \(\overrightarrow { a } ,\overrightarrow { b } \),

<

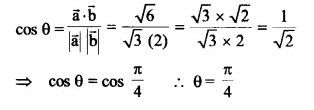
Ex 10.3 Class 12 Maths Question 2.
Find the angle between the vectors \(\hat { i } -2\hat { j } +3\hat { k } \quad and\quad 3\hat { i } -2\hat { j } +\hat { k } \)
Solution.
Let \(\overrightarrow { a } =\hat { i } -2\hat { j } +3\hat { k } \quad and\quad \overrightarrow { b } =3\hat { i } -2\hat { j } +\hat { k } \)
Let θ be the angle between \(\overrightarrow { a } ,\overrightarrow { b } \),

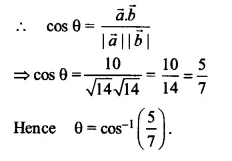
Ex 10.3 Class 12 Maths Question 3.
Find the projection of the vector \(\overrightarrow { i } -\overrightarrow { j } \), on the line represented by the vector \(\overrightarrow { i } +\overrightarrow { j } \),
Solution.
let \(\overrightarrow { a } =\hat { i } -\hat { j } \quad and\quad \overrightarrow { b } =\hat { i } +\hat { j } \)

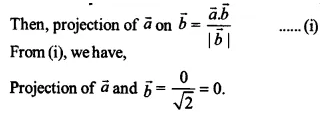
Ex 10.3 Class 12 Maths Question 4.
Find the projection of the vector \(\hat { i } +3\hat { j } +7\hat { k } \) on the vector \(7\hat { i } -\hat { j } +8\hat { k } \)
Solution.
let \(\overrightarrow { a } =\hat { i } +3\hat { j } +7\hat { k } \quad and\quad \overrightarrow { b } =7\hat { i } -\hat { j } +8\hat { k } \) then

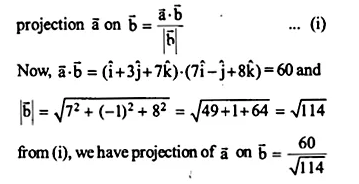
Ex 10.3 Class 12 Maths Question 5.
Show that each of the given three vectors is a unit vector \(\frac { 1 }{ 7 } \left( 2\hat { i } +3\hat { j } +6\hat { k } \right) ,\frac { 1 }{ 7 } \left( 3\hat { i } -6\hat { j } +2\hat { k } \right) ,\frac { 1 }{ 7 } \left( 6\hat { i } +2\hat { j } -3\hat { k } \right) \) Also show that they are mutually perpendicular to each other.
Solution.
\(Let\quad \overrightarrow { a } =\frac { 1 }{ 7 } \left( 2\hat { i } +3\hat { j } +6\hat { k } \right) ,\overrightarrow { b } =\frac { 1 }{ 7 } \left( 3\hat { i } -6\hat { j } +2\hat { k } \right) ,\overrightarrow { c } =\frac { 1 }{ 7 } \left( 6\hat { i } +2\hat { j } -3\hat { k } \right) \)

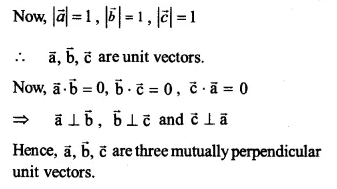
Ex 10.3 Class 12 Maths Question 6.
\(Find\left| \overrightarrow { a } \right| and\left| \overrightarrow { b } \right| if\left( \overrightarrow { a } +\overrightarrow { b } \right) \cdot \left( \overrightarrow { a } -\overrightarrow { b } \right) =8\quad and\left| \overrightarrow { a } \right| =8\left| \overrightarrow { b } \right| \)
Solution.
Given \(\left( \overrightarrow { a } +\overrightarrow { b } \right) \cdot \left( \overrightarrow { a } -\overrightarrow { b } \right) =8\)

Ex 10.3 Class 12 Maths Question 7.
Evaluate the product :
\(\left( 3\overrightarrow { a } -5\overrightarrow { b } \right) \cdot \left( 2\overrightarrow { a } +7\overrightarrow { b } \right) \)
Solution.
\(\left( 3\overrightarrow { a } -5\overrightarrow { b } \right) \cdot \left( 2\overrightarrow { a } +7\overrightarrow { b } \right) \)
\(=6\overrightarrow { a } .\overrightarrow { a } -10\overrightarrow { b } \overrightarrow { a } +21\overrightarrow { a } .\overrightarrow { b } -35\overrightarrow { b } .\overrightarrow { b } \)
\(=6{ \left| \overrightarrow { a } \right| }^{ 2 }-11\overrightarrow { a } \overrightarrow { b } -35{ \left| \overrightarrow { b } \right| }^{ 2 }\)

Ex 10.3 Class 12 Maths Question 8.
Find the magnitude of two vectors \(\overrightarrow { a } ,\overrightarrow { b } \) having the same magnitude and such that the angle between them is 60° and their scalar product is \(\frac { 1 }{ 2 }\)
Solution.
We know that \(\overrightarrow { a } .\overrightarrow { b } =\left| \overrightarrow { a } \right| \left| \overrightarrow { b } \right| cos\theta \)

Ex 10.3 Class 12 Maths Question 9.
Find \(\left| \overrightarrow { x } \right| \) , if for a unit vector \(\overrightarrow { a } ,(\overrightarrow { x } -\overrightarrow { a } )\cdot (\overrightarrow { x } +\overrightarrow { a } )=12\)
Solution.
Given
\(\overrightarrow { a } ,(\overrightarrow { x } -\overrightarrow { a } )\cdot (\overrightarrow { x } +\overrightarrow { a } )=12\)

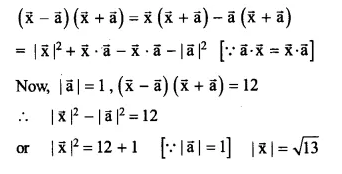
Ex 10.3 Class 12 Maths Question 10.
If \(\overrightarrow { a } =2\hat { i } +2\hat { j } +3\hat { k } ,\overrightarrow { b } =-\hat { i } +2\hat { j } +\hat { k } and\overrightarrow { c } =3\hat { i } +\hat { j } \) such that \(\overrightarrow { a } +\lambda \overrightarrow { b } \bot \overrightarrow { c } \) , then find the value of λ.
Solution.
Given
\(\overrightarrow { a } =2\hat { i } +2\hat { j } +3\hat { k } ,\overrightarrow { b } =-\hat { i } +2\hat { j } +\hat { k } and\overrightarrow { c } =3\hat { i } +\hat { j } \)

Ex 10.3 Class 12 Maths Question 11.
Show that \(\left| \overrightarrow { a } \right| \overrightarrow { b } +\left| \overrightarrow { b } \right| a\quad \bot \quad \left| \overrightarrow { a } \right| \cdot \overrightarrow { b } -\left| \overrightarrow { b } \right| a\) for any two non-zero vectors \(\overrightarrow { a } ,\overrightarrow { b } \)
Solution.
\(\overrightarrow { a } ,\overrightarrow { b } \) are any two non zero vectors

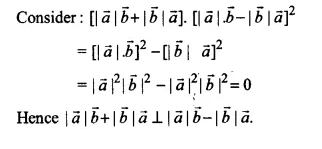
Ex 10.3 Class 12 Maths Question 12.
If \(\overrightarrow { a } \cdot \overrightarrow { a } =0\quad and\quad \overrightarrow { a } \cdot \overrightarrow { b } =0\), then what can be concluded about the vector \(\overrightarrow { b } \) ?
Solution.
\(\overrightarrow { a } \overrightarrow { a } =0\quad and\quad \overrightarrow { a } .\overrightarrow { b } =0 \),
=> \(\overrightarrow { b } \) = 0
Hence b is any vector.

Ex 10.3 Class 12 Maths Question 13.
If \(\overrightarrow { a } ,\overrightarrow { b } ,\overrightarrow { c } \) are the unit vector such that \(\overrightarrow { a } +\overrightarrow { b } +\overrightarrow { c } =0\) , then find the value of \(\overrightarrow { a } .\overrightarrow { b } +\overrightarrow { b } .\overrightarrow { c } +\overrightarrow { c } .\overrightarrow { a } \)
Solution.
We have
\(\overrightarrow { a } +\overrightarrow { b } +\overrightarrow { c } =0\)

Ex 10.3 Class 12 Maths Question 14.
If either vector \(\overrightarrow { a } =0\quad or\quad \overrightarrow { b } =0\) then \(\overrightarrow { a } .\overrightarrow { b } =0\). But the converse need not be true. Justify your answer with an example.
Solution.
Given: \(\overrightarrow { a } =0\quad or\quad \overrightarrow { b } =0\)
To prove: \(\overrightarrow { a } .\overrightarrow { b } =0\)

Ex 10.3 Class 12 Maths Question 15.
If the vertices A,B,C of a triangle ABC are (1,2,3) (-1,0,0), (0,1,2) respectively, then find ∠ABC.
Solution.
Let O be the origin then.
\(\frac { 1 }{ 2 }\)

Ex 10.3 Class 12 Maths Question 16.
Show that the points A (1,2,7), B (2,6,3) and C (3,10, -1) are collinear.
Solution.
The position vectors of points A, B, C are

Ex 10.3 Class 12 Maths Question 17.
Show that the vectors \(2\hat { i } -\hat { j } +\hat { k } ,\hat { i } -3\hat { j } -5\hat { k } \) and \(\left( 3\hat { i } -4\hat { j } -4\hat { k } \right) \) from the vertices of a right angled triangle.
Solution.
The position vectors of the points A, B and C are
\(2\hat { i } -\hat { j } +\hat { k } ,\hat { i } -3\hat { j } -5\hat { k } \) and \(\left( 3\hat { i } -4\hat { j } -4\hat { k } \right) \)

Ex 10.3 Class 12 Maths Question 18.
If \(\overrightarrow { a } \) is a non-zero vector of magnitude ‘a’ and λ is a non- zero scalar, then λ \(\overrightarrow { a } \) is unit vector if
(a) λ = 1
(b) λ = – 1
(c) a = |λ|
(d) a = \(\frac { 1 }{ \left| \lambda \right| } \)
Solution.
\(\left| \overrightarrow { a } \right| =a\)
Given : \(\lambda \overrightarrow { a } \) is a unit vectors

NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4

Ex 10.4 Class 12 Maths Question 1.
Find \(\left| \overrightarrow { a } \times \overrightarrow { b } \right| ,if\quad \overrightarrow { a } =\hat { i } -7\hat { j } +7\hat { k } \quad and\quad \overrightarrow { b } =3\hat { i } -2\hat { j } +2\hat { k } \)
Solution.
Given
\(\overrightarrow { a } =\hat { i } -7\hat { j } +7\hat { k } \quad and\quad \overrightarrow { b } =3\hat { i } -2\hat { j } +2\hat { k } \)

<

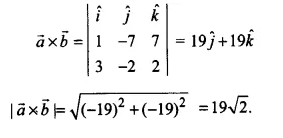
NCERT Maths Class 12 Chapter 10

Ex 10.4 Class 12 Maths Question 2.
Find a unit vector perpendicular to each of the vector \(\overrightarrow { a } +\overrightarrow { b } \quad and\quad \overrightarrow { a } -\overrightarrow { b } \), where \(\overrightarrow { a } =3\hat { i } +2\hat { j } +2\hat { k } \quad and\quad \overrightarrow { b } =\hat { i } +2\hat { j } -2\hat { k } \)
Solution.
we have
\(\overrightarrow { a } =3\hat { i } +2\hat { j } +2\hat { k } \quad and\quad \overrightarrow { b } =\hat { i } +2\hat { j } -2\hat { k } \)

Ex 10.4 Class 12 Maths Question 3.
If a unit vector \(\overrightarrow { a } \) makes angle \(\frac { \pi }{ 3 } with\quad \hat { i } ,\frac { \pi }{ 4 } with\quad \hat { j } \) and an acute angle θ with \(\overrightarrow { k } \),then find θ and hence the components of \(\overrightarrow { a } \).
Solution.
\(Let\quad \overrightarrow { a } ={ a }_{ 1 }\hat { i } +{ a }_{ 2 }\hat { j } +{ a }_{ 3 }\hat { k } such\quad that\quad \left| \overrightarrow { a } \right| =1\)

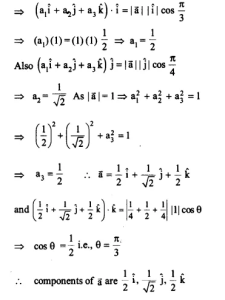
Ex 10.4 Class 12 Maths Question 4.
Show that \(\left( \overrightarrow { a } -\overrightarrow { b } \right) \times \left( \overrightarrow { a } +\overrightarrow { b } \right) =2\left( \overrightarrow { a } \times \overrightarrow { b } \right) \)
Solution.
LHS = \(\left( \overrightarrow { a } -\overrightarrow { b } \right) \times \left( \overrightarrow { a } +\overrightarrow { b } \right) \)

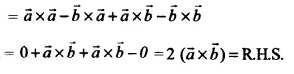
Ex 10.4 Class 12 Maths Question 5.
Find λ and μ if
\(\left( 2\hat { i } +6\hat { j } +27\hat { k } \right) \times \left( \hat { i } +\lambda \hat { j } +\mu \hat { k } \right) =0\)
Solution.
\(\left( 2\hat { i } +6\hat { j } +27\hat { k } \right) \times \left( \hat { i } +\lambda \hat { j } +\mu \hat { k } \right) =0\)

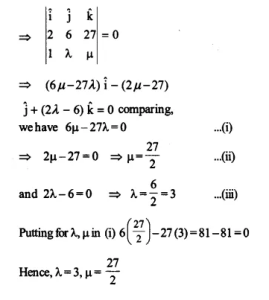
Ex 10.4 Class 12 Maths Question 6.
Given that \(\overrightarrow { a } .\overrightarrow { b } =0\quad and\quad \overrightarrow { a } \times \overrightarrow { b } =0\). What can you conclude about the vectors \(\overrightarrow { a } ,\overrightarrow { b } \) ?
Solution.
\(\overrightarrow { a } .\overrightarrow { b } =0\quad and\quad \overrightarrow { a } \times \overrightarrow { b } =0\)

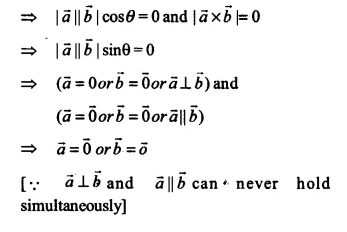
Ex 10.4 Class 12 Maths Question 7.
Let the vectors \(\overrightarrow { a } ,\overrightarrow { b } ,\overrightarrow { c } \) are given \({ a }_{ 1 }\hat { i } +{ a }_{ 2 }\hat { j } +{ a }_{ 3 }\hat { k } ,{ b }_{ 1 }\hat { i } +{ b }_{ 2 }\hat { j } +{ b }_{ 3 }\hat { k } ,{ c }_{ 1 }\hat { i } +{ c }_{ 2 }\hat { j } +{ c }_{ 3 }\hat { k } \). Then show that \(\overrightarrow { a } \times \left( \overrightarrow { b } +\overrightarrow { c } \right) \)\(=\overrightarrow { a } \times \overrightarrow { b } +\overrightarrow { a } \times \overrightarrow { c } \)
Solution.
Given
\(\overrightarrow { a } ,\overrightarrow { b } ,\overrightarrow { c } \) are given \({ a }_{ 1 }\hat { i } +{ a }_{ 2 }\hat { j } +{ a }_{ 3 }\hat { k } ,{ b }_{ 1 }\hat { i } +{ b }_{ 2 }\hat { j } +{ b }_{ 3 }\hat { k } ,{ c }_{ 1 }\hat { i } +{ c }_{ 2 }\hat { j } +{ c }_{ 3 }\hat { k } \)

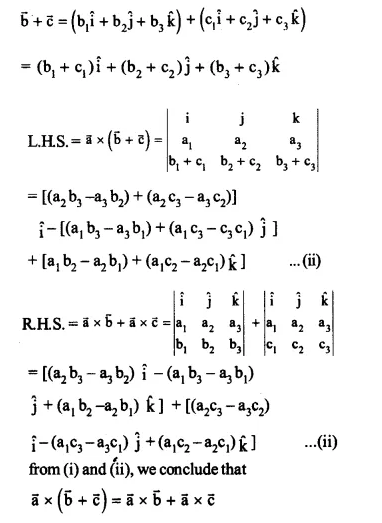
Ex 10.4 Class 12 Maths Question 8.
If either \(\overrightarrow { a } =0\quad or\quad \overrightarrow { b } =0\quad then\quad \hat { a } \times \hat { b } =0\).Is the
converse true? Justify your answer with an example.
Solution.
\(\overrightarrow { a } =0\Rightarrow \left| \overrightarrow { a } \right| =0\)

Ex 10.4 Class 12 Maths Question 9.
Find the area of the triangle with vertices A (1,1,2), B (2,3,5) and C (1,5,5).
Solution.
A (1,1,2), B (2,3,5) and C (1,5,5).

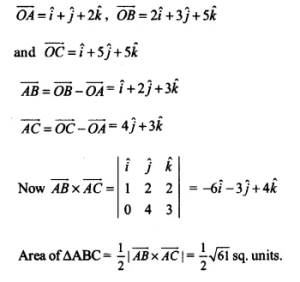
Ex 10.4 Class 12 Maths Question 10.
Find the area of the parallelogram whose adjacent sides are determined by the vectors \(\overrightarrow { a } =\hat { i } -\hat { j } +3\hat { k } ,\overrightarrow { b } =2\hat { i } -7\hat { j } +\hat { k } \)
Solution.
We have \(\overrightarrow { a } =\hat { i } -\hat { j } +3\hat { k } ,\overrightarrow { b } =2\hat { i } -7\hat { j } +\hat { k } \)

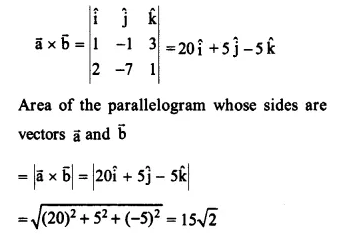
Ex 10.4 Class 12 Maths Question 11.
Let the vectors\(\overrightarrow { a } ,\overrightarrow { b } \) such that \(\left| \overrightarrow { a } \right| =3,\left| \overrightarrow { b } \right| =\frac { \sqrt { 2 } }{ 3 } \) then \(\overrightarrow { a } \times \overrightarrow { b } \) is a unit vector if the angle between \(\overrightarrow { a } ,\overrightarrow { b } \) is
(a) \(\frac { \pi }{ 6 } \)
(b) \(\frac { \pi }{ 4 } \)
(c) \(\frac { \pi }{ 3 } \)
(d) \(\frac { \pi }{ 2 } \)
Solution.
Given
\(\left| \overrightarrow { a } \times \overrightarrow { b } \right| =1\)
\(\left| \overrightarrow { a } \right| =3,\left| \overrightarrow { b } \right| =\frac { \sqrt { 2 } }{ 3 } \)

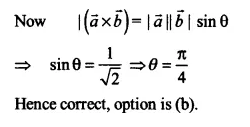
Ex 10.4 Class 12 Maths Question 12.
Area of a rectangles having vertices
\(A\left( -\hat { i } +\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) ,B\left( \hat { i } +\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) ,\)
\(C\left( \hat { i } -\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) ,D\left( -\hat { i } -\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) ,\)
(a) \(\frac { 1 }{ 2 }\) sq units
(b) 1sq.units
(c) 2sq.units
(d) 4sq.units
Solution.
\(\overrightarrow { OA } =\left( -\hat { i } +\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) \)
\(\overrightarrow { OB } =\left( \hat { i } +\frac { 1 }{ 2 } \hat { j } +4\hat { k } \right) \)

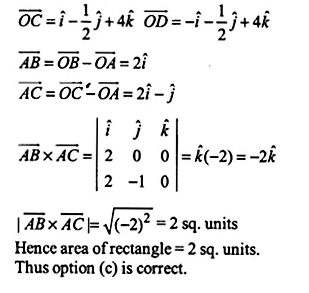
NCERT Class 12 Maths

Class 12 Maths Chapters | Maths Class 12 Chapter 10

Chapterwise NCERT Solutions for Class 12 Maths

NCERT Solutions For Class 12 Maths Chapter 1 Relations and Functions
NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions
NCERT Solutions For Class 12 Maths Chapter 3 Matrix
NCERT Solutions For Class 12 Maths Chapter 4 Determinants
NCERT Solutions For Class 12 Maths Chapter 5 Continuity and Differentiability
NCERT Solutions For Class 12 Maths Chapter 6 Application of Derivatives
NCERT Solutions For Class 12 Maths Chapter 7 Integrals
NCERT Solutions For Class 12 Maths Chapter 8 Application of Integrals
NCERT Solutions For Class 12 Maths Chapter 9 Differential Equations
NCERT Solutions For Class 12 Maths Chapter 10 Vector Algebra
NCERT Solutions For Class 12 Maths Chapter 11 Three-dimensional Geometry
NCERT Solutions For Class 12 Maths Chapter 12 Linear Programming
NCERT Solutions For Class 12 Maths Chapter 13 Probability

NCERT Solutions for Class 12 All Subjects	NCERT Solutions for Class 10 All Subjects
NCERT Solutions for Class 11 All Subjects	NCERT Solutions for Class 9 All Subjects

NCERT SOLUTIONS