NCERT Solutions | Class 12 Maths Chapter 2

NCERT Solutions | Class 12 Maths Chapter 2 | Inverse Trigonometric Functions 

CBSE Solutions | Maths Class 12

Check the below NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Pdf free download. NCERT Solutions Class 12 Maths  were prepared based on the latest exam pattern. We have Provided Inverse Trigonometric Functions Class 12 Maths NCERT Solutions to help students understand the concept very well.

NCERT | Class 12 Maths

NCERT Solutions Class 12 Maths

Book:	National Council of Educational Research and Training (NCERT)
Board:	Central Board of Secondary Education (CBSE)
Class:	12th
Subject:	Maths
Chapter:	2
Chapters Name:	Inverse Trigonometric Functions
Medium:	English

Inverse Trigonometric Functions | Class 12 Maths | NCERT Books Solutions

You can refer to MCQ Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions to revise the concepts in the syllabus effectively and improve your chances of securing high marks in your board exams.

NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.1

Ex 2.1 Class 12 Maths Question 1-10.
Find the principal values of the following:
(1) \(\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \)
(2) \(\cos ^{ -1 }{ \left( \frac { \sqrt { 3 } }{ 2 } \right) } \)
(3) \(\csc ^{ -1 }{ (2) } \)
(4) \(\tan ^{ -1 }{ \left( -\sqrt { 3 } \right) } \)
(5) \(\cos ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \)
(6) \(\tan ^{ -1 }{ (-1) } \)
(7) \(\sec ^{ -1 }{ \left( \frac { 2 }{ \sqrt { 3 } } \right) } \)
(8)\(\cot ^{ -1 }{ \left( \sqrt { 3 } \right) } \)
(9) \(\cos ^{ -1 }{ \left( -\frac { 1 }{ \sqrt { 2 } } \right) } \)
(10) \(\csc ^{ -1 }{ \left( -\sqrt { 2 } \right) } \)
Solution.
(1) Let \(\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \) = y
∴ \(sin\quad y=-\frac { 1 }{ 2 } =-sin\frac { \pi }{ 6 } =sin\left( -\frac { \pi }{ 6 } \right) \)
the range of principal value of sin^-1 is

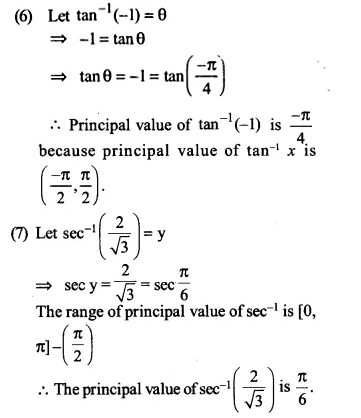
Ex 2.1 Class 12 Maths Question 11-12.
Find the principal values of the following:
(11) \(\tan ^{ -1 }{ (1) } +\cos ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } +\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \)
(12) \(\cos ^{ -1 }{ \left( \frac { 1 }{ 2 } \right) } +2\sin ^{ -1 }{ \left( \frac { 1 }{ 2 } \right) } \)
Solution.
(11) \(\tan ^{ -1 }{ (1) } +\cos ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } +\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \)
Now tan^-1 (1) = \(\frac { \pi }{ 4 } \)
∴the range of principal value branch of

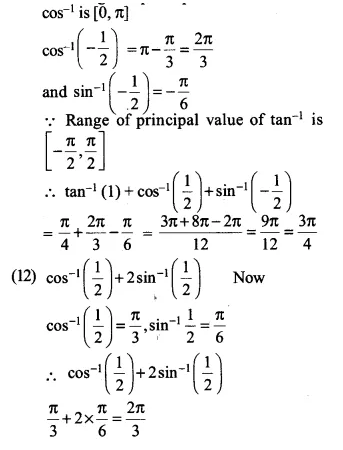
Ex 2.1 Class 12 Maths Question 13.
If sin^-1 x = y, then
(a) 0 ≤ y ≤ π
(b) \(-\frac { \pi }{ 2 } \le y\le \frac { \pi }{ 2 } \)
(c) 0 < y < π
(d) \(-\frac { \pi }{ 2 } <y<\frac { \pi }{ 2 } \)
Solution.
The range of principal value of sin is \(\left[ -\frac { \pi }{ 2 } ,\frac { \pi }{ 2 } \right] \)
∴ if sin^-1 x = y then
\(-\frac { \pi }{ 2 } \le y\le \frac { \pi }{ 2 } \)
Option (b) is correct

Ex 2.1 Class 12 Maths Question 14.
\(\tan ^{ -1 }{ \sqrt { 3 } -\sec ^{ -1 }{ (-2) } } \) is equal to
(a) π
(b) \(-\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 3 } \)
(d) \(\frac { 2\pi }{ 3 } \)
Solution.
\(\tan ^{ -1 }{ \sqrt { 3 } =\frac { \pi }{ 3 } ,\sec ^{ -1 }{ (-2) } } =\pi -\frac { \pi }{ 3 } =\frac { 2\pi }{ 3 } \)
∴ Principal values of sec^-1 is [0,π] – \(\left\{ \frac { \pi }{ 2 } \right\} \)
\(\tan ^{ -1 }{ \sqrt { 3 } – } \sec ^{ -1 }{ (-2) } =\frac { \pi }{ 3 } -\frac { 2\pi }{ 3 } =-\frac { \pi }{ 3 } \)
Option (b) is correct

 

NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.2

Ex 2.2 Class 12 Maths Question 1.
\(3\sin ^{ -1 }{ x=\sin ^{ -1 }{ (3x-4x^{ 3 });x\in \left[ -\frac { 1 }{ 2 } ,\frac { 1 }{ 2 } \right] } } \)
Solution.
Let sin^-1 x = θ
sin θ = x sin 3θ = 3 sin θ – 4 sin³ θ
sin 3θ = 3x – 4x³
3θ = sin^-1 (3x – 4x³)
or \(3\sin ^{ -1 }{ x=\sin ^{ -1 }{ (3x-4x^{ 3 });x\in \left[ -\frac { 1 }{ 2 } ,\frac { 1 }{ 2 } \right] } } \)

<

Ex 2.2 Class 12 Maths Question 2.
\(3\cos ^{ -1 }{ x } =\cos ^{ -1 }{ \left( { 4x }^{ 3 }-3x \right) ,x\in \left[ \frac { 1 }{ 2 } ,1 \right] } \)
Solution.
Let cos^-1 x = θ
x = cos θ
R.H.S= cos^-1 (4x³ – 3cosx)
= cos^-1 (4 cos³θ – 3 cosθ)
= cos^-1 (cos 3θ) [∴ cos 3θ = 4 cos³ θ – 3 cos θ]
= 3θ
= 3 cos^-1 x
= L.H.S.

Ex 2.2 Class 12 Maths Question 3.
\(\tan ^{ -1 }{ \frac { 2 }{ 11 } } +\tan ^{ -1 }{ \frac { 7 }{ 24 } } =\tan ^{ -1 }{ \frac { 1 }{ 2 } } \)
Solution.
L.H.S = \(\tan ^{ -1 }{ \frac { 2 }{ 11 } } +\tan ^{ -1 }{ \frac { 7 }{ 24 } } \)
= \(\tan ^{ -1 }{ \left[ \frac { \frac { 2 }{ 11 } +\frac { 7 }{ 24 } }{ 1-\frac { 2 }{ 11 } \times \frac { 7 }{ 24 } } \right] } \)
= \(\tan ^{ -1 }{ \left[ \frac { 1 }{ 2 } \right] } \)
= R.H.S

Ex 2.2 Class 12 Maths Question 4.
\(2\tan ^{ -1 }{ \frac { 1 }{ 2 } } +\tan ^{ -1 }{ \frac { 1 }{ 7 } } =\tan ^{ -1 }{ \frac { 31 }{ 17 } } \)
Solution.
L.H.S =
\(2\tan ^{ -1 }{ \frac { 1 }{ 2 } } +\tan ^{ -1 }{ \frac { 1 }{ 7 } } \)

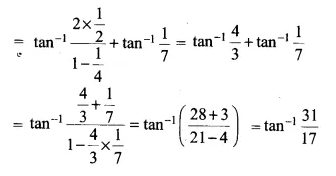
Ex 2.2 Class 12 Maths Question 5.
Write the function in the simplest form
\(\tan ^{ -1 }{ \left( \frac { \sqrt { 1+{ x }^{ 2 }-1 } }{ x } \right) } ,x\neq 0\)
Solution.
Putting x = θ
∴ θ = tan^-1 x

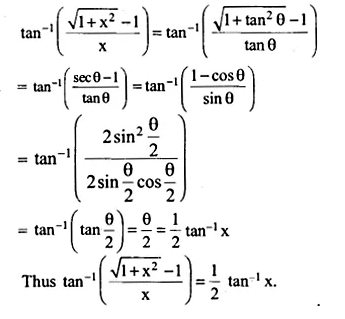
Ex 2.2 Class 12 Maths Question 6.
\(\tan ^{ -1 }{ \left( \frac { 1 }{ \sqrt { { x }^{ 2 }-1 } } \right) ,\left| x \right| } >1\)
Solution.
Given expression
\(\tan ^{ -1 }{ \left( \frac { 1 }{ \sqrt { { x }^{ 2 }-1 } } \right) ,\left| x \right| } >1\)
Let x = secθ

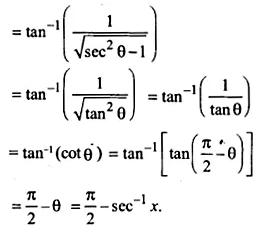
Ex 2.2 Class 12 Maths Question 7.
\(\tan ^{ -1 }{ \left( \sqrt { \frac { 1-cosx }{ 1+cosx } } \right) } ,0<x<\pi \)
Solution.
\(\tan ^{ -1 }{ \left( \sqrt { \frac { 1-cosx }{ 1+cosx } } \right) } ,0<x<\pi \)
= \(\tan ^{ -1 }{ \left[ \sqrt { \frac { { 2sin }^{ 2 }\frac { x }{ 2 } }{ { 2cos }^{ 2 }\frac { x }{ 2 } } } \right] } \)

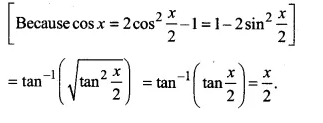
Ex 2.2 Class 12 Maths Question 8.
\(\tan ^{ -1 }{ \left( \frac { cosx-sinx }{ cosx+sinx } \right) ,0<x<\pi } \)
Solution.
\(\tan ^{ -1 }{ \left( \frac { cosx-sinx }{ cosx+sinx } \right) ,0<x<\pi } \)
Dividing numerator and denominator by cos x

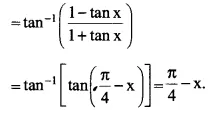
Ex 2.2 Class 12 Maths Question 9.
\(\tan ^{ -1 }{ \left( \frac { x }{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } } \right) ,\left| x \right| } <a\)
Solution.
Let x = a sinθ
=> \(\\ \frac { x }{ a } \) = sinθ

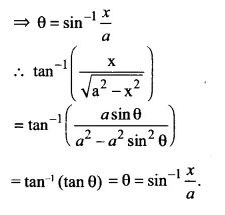
Ex 2.2 Class 12 Maths Question 10.
\(\tan ^{ -1 }{ \left[ \frac { { 3a }^{ 2 }-{ x }^{ 3 } }{ { a }^{ 3 }-{ 3ax }^{ 2 } } \right] ,a>0;\frac { -a }{ \sqrt { 3 } } <x,<\frac { a }{ \sqrt { 3 } } } \)
Solution.
Put x = a tanθ,
we get

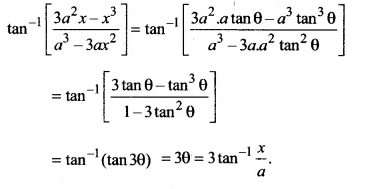
Ex 2.2 Class 12 Maths Question 11.
Find the value of the following
\(\tan ^{ -1 }{ \left[ 2cos\left( 2\sin ^{ -1 }{ \frac { 1 }{ 2 } } \right) \right] } \)
Solution.
\(\tan ^{ -1 }{ \left[ 2cos\left( 2\sin ^{ -1 }{ \frac { 1 }{ 2 } } \right) \right] } \)
= \(\tan ^{ -1 }{ \left[ 2cos2.\frac { \pi }{ 6 } \right] } \)

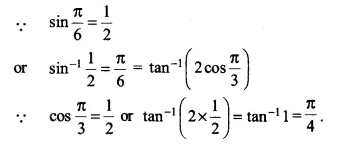
Ex 2.2 Class 12 Maths Question 12.
cot[tan^-1 a + cot^-1 a]
Solution.
Given
cot[tan^-1 a + cot^-1 a]
= \(cot\left( \tan ^{ -1 }{ a } +\tan ^{ -1 }{ \frac { 1 }{ a } } \right) \)

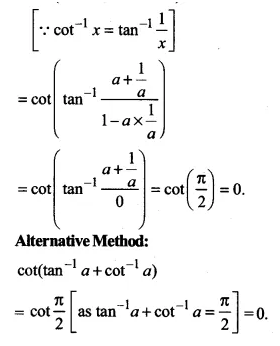
Ex 2.2 Class 12 Maths Question 13.
\(tan\frac { 1 }{ 2 } \left[ \sin ^{ -1 }{ \frac { 2x }{ 1+{ x }^{ 2 } } +\cos ^{ -1 }{ \frac { 1-{ y }^{ 2 } }{ 1+{ y }^{ 2 } } } } \right] \left| x \right| <1,y>0\quad and\quad xy<1\)
Solution.
Putting x = tanθ
=> tan^-1 x = θ

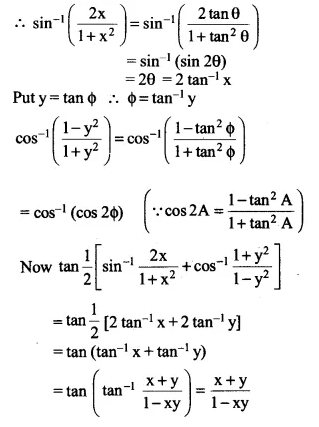
Ex 2.2 Class 12 Maths Question 14.
If \(sin\left( \sin ^{ -1 }{ \frac { 1 }{ 5 } } +\cos ^{ -1 }{ x } \right) =1\) then find the value of x
Solution.
\(sin\left( \sin ^{ -1 }{ \frac { 1 }{ 5 } } +\cos ^{ -1 }{ x } \right) =sin\frac { \pi }{ 2 } \)

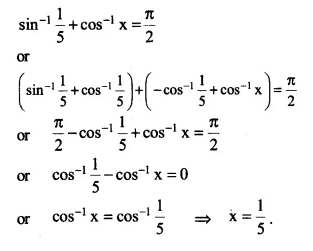
Ex 2.2 Class 12 Maths Question 15.
If \(\tan ^{ -1 }{ \frac { x-1 }{ x-2 } } +\tan ^{ -1 }{ \frac { x+1 }{ x+2 } } =\frac { \pi }{ 4 } \) then find the value of x
Solution.
L.H.S
\(\tan ^{ -1 }{ \frac { x-1 }{ x-2 } } +\tan ^{ -1 }{ \frac { x+1 }{ x+2 } } =\frac { \pi }{ 4 } \)

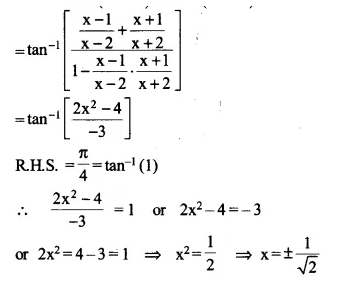
Ex 2.2 Class 12 Maths Question 16.
\(\sin ^{ -1 }{ \left( sin\frac { 2\pi }{ 3 } \right) } \)
Solution.
\(\sin ^{ -1 }{ \left( sin\frac { 2\pi }{ 3 } \right) } \)
= \(\sin ^{ -1 }{ \left( sin\left( \pi -\frac { \pi }{ 3 } \right) \right) } \)
= \(\sin ^{ -1 }{ \left( sin\left( \frac { \pi }{ 3 } \right) \right) } =\frac { \pi }{ 3 } \)

Ex 2.2 Class 12 Maths Question 17.
\(\tan ^{ -1 }{ \left( tan\frac { 3\pi }{ 4 } \right) } \)
Solution.
\(\tan ^{ -1 }{ \left( tan\frac { 3\pi }{ 4 } \right) } \)
= \(\tan ^{ -1 }{ \left( sin\frac { 3\pi }{ 4 } \right) } \)
= \(\tan ^{ -1 }{ tan\left( \pi -\frac { \pi }{ 4 } \right) } \)

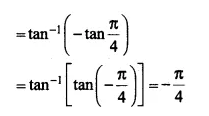
Ex 2.2 Class 12 Maths Question 18.
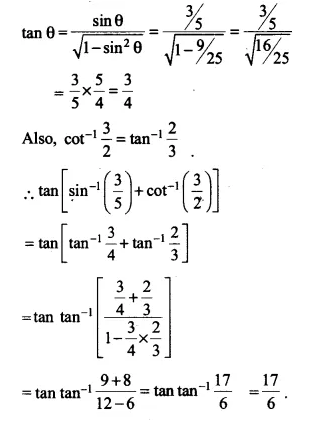
\(tan\left( \sin ^{ -1 }{ \frac { 3 }{ 5 } +\cot ^{ -1 }{ \frac { 3 }{ 2 } } } \right) \)
Solution.
\(tan\left( \sin ^{ -1 }{ \frac { 3 }{ 5 } +\cot ^{ -1 }{ \frac { 3 }{ 2 } } } \right) \)
Let \(\sin ^{ -1 }{ \frac { 3 }{ 5 } = } \theta \)
sinθ = \(\\ \frac { 3 }{ 5 } \)

Ex 2.2 Class 12 Maths Question 19.
\(\cos ^{ -1 }{ \left( cos\frac { 7\pi }{ 6 } \right) } \) is equal to
(a) \(\frac { 7\pi }{ 6 } \)
(b) \(\frac { 5\pi }{ 6 } \)
(c) \(\frac { \pi }{ 5 } \)
(d) \(\frac { \pi }{ 6 } \)
Solution.
\(\cos ^{ -1 }{ \left( cos\frac { 7\pi }{ 6 } \right) } \)
= \(\cos ^{ -1 }{ cos\left( \pi +\frac { \pi }{ 6 } \right) } \)

Ex 2.2 Class 12 Maths Question 20.
\(sin\left[ \frac { \pi }{ 3 } -\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \right] \) is equal to
(a) \(\\ \frac { 1 }{ 2 } \)
(b) \(\\ \frac { 1 }{ 3 } \)
(c) \(\\ \frac { 1 }{ 4 } \)
(d) 1
Solution.
\(sin\left[ \frac { \pi }{ 3 } -\sin ^{ -1 }{ \left( -\frac { 1 }{ 2 } \right) } \right] \)

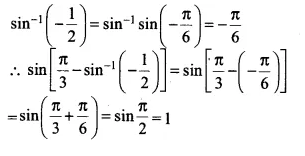
Ex 2.2 Class 12 Maths Question 21.
\(\tan ^{ -1 }{ \sqrt { 3 } -\cot ^{ -1 }{ \left( -\sqrt { 3 } \right) } } \) is equal to
(a) π
(b) \(-\frac { \pi }{ 2 } \)
(c) 0
(d) 2√3
Solution.
\(\tan ^{ -1 }{ \sqrt { 3 } -\cot ^{ -1 }{ \left( -\sqrt { 3 } \right) } } \)

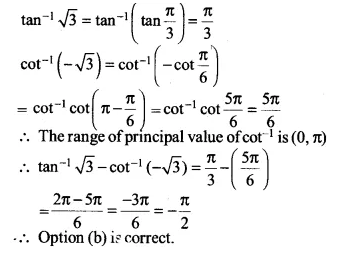
NCERT Class 12 Maths

Class 12 Maths Chapters | Maths Class 12 Chapter 2

Chapterwise NCERT Solutions for Class 12 Maths

NCERT Solutions For Class 12 Maths Chapter 1 Relations and Functions
NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions
NCERT Solutions For Class 12 Maths Chapter 3 Matrix
NCERT Solutions For Class 12 Maths Chapter 4 Determinants
NCERT Solutions For Class 12 Maths Chapter 5 Continuity and Differentiability
NCERT Solutions For Class 12 Maths Chapter 6 Application of Derivatives
NCERT Solutions For Class 12 Maths Chapter 7 Integrals
NCERT Solutions For Class 12 Maths Chapter 8 Application of Integrals
NCERT Solutions For Class 12 Maths Chapter 9 Differential Equations
NCERT Solutions For Class 12 Maths Chapter 10 Vector Algebra
NCERT Solutions For Class 12 Maths Chapter 11 Three-dimensional Geometry
NCERT Solutions For Class 12 Maths Chapter 12 Linear Programming
NCERT Solutions For Class 12 Maths Chapter 13 Probability

NCERT Solutions for Class 12 All Subjects	NCERT Solutions for Class 10 All Subjects
NCERT Solutions for Class 11 All Subjects	NCERT Solutions for Class 9 All Subjects

NCERT SOLUTIONS