NCERT Solutions | Class 11 Arthshastra Chapter 7

NCERT Solutions | Class 11 Arthshastra अर्थशास्त्र में सांख्यिकी (Sankhyiki) Chapter 7 | सहसंबंध 

CBSE Solutions | Arthshastra Class 11

Check the below NCERT Solutions for Class 11 Arthshastra अर्थशास्त्र में सांख्यिकी (Sankhyiki) Chapter 7 सहसंबंध Pdf free download. NCERT Solutions Class 11 Arthshastra  were prepared based on the latest exam pattern. We have Provided सहसंबंध Class 11 Arthshastra NCERT Solutions to help students understand the concept very well.

NCERT | Class 11 Arthshastra अर्थशास्त्र में सांख्यिकी (Sankhyiki)

NCERT Solutions Class 11 Arthshastra

Book:	National Council of Educational Research and Training (NCERT)
Board:	Central Board of Secondary Education (CBSE)
Class:	11
Subject:	Arthshastra
Chapter:	7
Chapters Name:	सहसंबंध
Medium:	Hindi

सहसंबंध | Class 11 Arthshastra | NCERT Books Solutions

You can refer to MCQ Questions for Class 11 Arthshastra अर्थशास्त्र में सांख्यिकी (Sankhyiki) Chapter 7 सहसंबंध to revise the concepts in the syllabus effectively and improve your chances of securing high marks in your board exams.

NCERT Solutions for Class 11 Economics Statistics for Economics Chapter 7 (Hindi Medium)

प्रश्न अभ्यास

(पाठ्यपुस्तक से)

प्र.1. कद (फुटों में) तथा वजन (किलोग्राम में) के बीच सहसंबंध गुणांक की इकाई है:

(क) कि. ग्रा/फुट
(ख) प्रतिशत
(ग) अविद्यमान

उत्तर :
(ग) अविद्यमान

प्र.2. सरल सहसंबंध गुणांक का परास निम्नलिखित होगा

(क) 0 से अनंत तक
(ख) -1 से +1 तक
(ग) ऋणात्मक अनंत से धनात्मक अनंत तक

उत्तर :
(ख) -1 से +1 तक

प्र.3. यदि r_xy धनात्मक है तो x और y के बीच का संबंध इस प्रकार का होता है।

(क) जब y बढ़ता है तो x बढ़ता है।
(ख) जब y घटता है तो x बढ़ता है।
(ग) जब y बढ़ता है तो x नहीं बदलता है।

उत्तर :
(क) जब y बढ़ता है तो x बढ़ता है।

प्र.4. यदि r_xy = 0 तब चर x और y के बीचः

(क) रेखीय संबंध होगा।
(ख) रेखीय संबंध नहीं होगा
(ग) स्वतंत्र होगा

उत्तर :
(ख) रेखीय संबंध नहीं होगा

प्र.5. निम्नलिखित तीनों मापों में कौन-सा माप किसी भी प्रकार के संबंध की माप कर सकता है।

(क) कार्ल पियरसन सहसंबंध गुणांक
(ख) स्पीयरमैन का कोटि सहसंबंध
(ग) प्रकीर्ण आरेख

उत्तर :
(ख) स्पीयरमैन का कोटि सहसंबंध

प्र.6. यदि परिशुद्ध रूप में मापित आँकड़े उपलब्ध हों, तो सरल सहसंबंध गुणांकः

(क) कोटि सहसंबंध गुणांक से अधिक सही होता है।
(ख) कोटि सहसंबंध गुणांक से कम सही होता है।
(ग) कोटि सहसंबंध की ही भाँति सही होती है।

उत्तर :
(ग) कोटि सहसंबंध की ही भाँति सही होता है।

प्र.7. साहचर्य के माप के लिए r को सहप्रसरण से अधिक प्राथमिकता क्यों दी जाती है?
उत्तर :
साहचर्य का माप x और y के बीच सहसंबंध गुणांक का चिह्न निश्चित करता है। मानक विचलन सदा धनात्मक होते हैं। जब सहप्रसरण शून्य होता है तो सहसंबंध भी शून्य होता है। सहसंबंध को सहप्रसरण से साहचर्य के माने के लिए अधिक प्राथमिकता दी जाती है क्योंकि

(क) यह धनात्मक ऋणात्मक और शून्य सहसंबंध के विषय में बताता है।
(ख) सहसंबंध मूलों और पैमानों से स्वतंत्र होते हैं।

प्र.8. क्या आँकड़ों के प्रकार के आधार पर r_, -1 तथा + 1 के बाहर स्थित हो सकता है?
उत्तर :
r (+1∠ r- 1) + 1 और -1 के बीच में स्थित होता है और यदि यह + 1 से बाहर हो तो इसका अर्थ है कि दो चरों में संबंध आरेखीय है। अत: इसका विवेचन करते हुए हमें यह याद रखना होगा कि अवश्य इसमें कुछ त्रुटियाँ हैं।

प्र.9, क्या सहसंबंध के द्वारा कार्यकारण संबंध की जानकारी मिलती है? 4
उत्तर :
नहीं सहसंबंध द्वारा कार्यकारण की जानकारी नहीं मिलती। अकसर विद्यार्थी यह विश्वास करने लगते हैं कि सहसंबंध दो चरों में वहाँ सहसबंधं सुझाता है जहाँ एक का कारण दूसरा है। उदाहरण: यह वस्तु की माँगी गई मात्रा और कीमत में सहसंबंध स्पष्टः कीमत में वृद्धि तथा माँगी गई मात्रा में कमी का कारण है और इसके विपरीत भी। कीमत में परिवर्तन माँगी गई मात्रा में परिवर्तन लाता है। परंतु जिस बिंदु पर ज्यादा बल देने की आवश्यकता है वह यह है कि चरों के बीच कारण और प्रभाव संबंध सहसंबंध के सिद्धांत में कोई भी पूर्व-स्थिति नहीं है। सहसंबंध दो चरों के बीच किसी कारण और प्रभाव संबंध के साथ या उसके बिना, संबंध की कोटि और तीव्रता को मापता है। सहसंबंध दो या दो से अधिक चर-मूलों में पारस्परिक संबंध की दिशा तथा मात्रा का अकात्मक माप है। परंतु सहसंबंध की उपस्थिति से यह नहीं मान लेना चाहिए कि दोनों चरों में आवश्यक रूप से प्रत्यक्ष कारण तथा परिणाम संबंध है। सह-संबंध सदैव कारण–परिणाम संबंध से ही उत्पन्न नहीं होता। परंतु कारण-परिणाम संबंध होने पर निश्चित रूप से सहसंबंध पाया जाता है।

प्र.10. सरल सहसंबंध गुणांक की तुलना में कोटि सहसंबंध गुणांक कब अधिक परिशुद्ध होता है?
उत्तर :
सरल सहसंबंध गुणांक की तुलना में कोटि सहसंबंध गुणांक अधिक परिशुद्ध होता है क्योंकि

1. इस विधि का उस स्थिति में भी सुगमता से प्रयोग किया जाता है जबकि आँकड़ों के स्थान पर केवल श्रेणियाँ ही दी गई हों तथा साधारण गुणात्मक श्रृंखलाओं के ढीले सहसंबंध अनुमान लगाने के लिए भी प्रयोग किया जा सकता है।
2. स्पीयरमैन श्रेणी अंतर सह-संबंध विधि पियरसन के सह-संबंध गुणांक की अपेक्षा समझने में सरल है।
3. यह विधि गुणात्मक चरों की अच्छाई, बुराई, बुद्धिमत्ता, सुंदरता व पवित्रता आदि के सह-संबंधों को ज्ञात करने के लिए श्रेष्ठ है।

प्र.11. क्या शून्य सहसंबंध का अर्थ स्वतंत्रता है?
उत्तर :
शून्य सहसंबंध का अर्थ स्वतंत्रता नहीं है अपितु इसका अर्थ रेखीय । सहसंबंध की स्वतंत्रता है। दो चरों में आरेखीय सहसंबंध होने पर जब उन्हें प्रकीर्ण आरेख पर दर्शाया जायेगा। तो वे शून्य सहसंबंध दर्शायेंगे तथा जब उन्हें पियरसन या स्पीयरमैन विधि से निकाला जाता है तो यह निम्न सहसंबंध का मान देगा। नीचे दी गई आकृति के द्वारा इसे समझा जा सकता है।

इसे शून्य सहसंबंध माना जायेगा, जबकि एक स्तर तक x और y धनात्मक रूप से संबंधित है तथा तदुपरांत उनमें ऋणात्मक सहसंबंध है।

प्र.12. क्या सरल सहसंबंध गुणांक किसी भी प्रकार के संबंध को माप सकता है?
उत्तर :
नहीं, सरल सहसंबध गुणाक केवल रेखीय सहसंबंध माप सकता है।

(क) यह आरेखीय सहसंबंध नहीं माप सकता।
(ख) यह ऐसे चरों के बीच सहसंबंध ज्ञात नहीं कर सकता जो संख्यात्मक रूप में व्यक्त नहीं किये जा सकते।
(ग) यह धनात्मक, ऋणात्मक तथा रेखीय सहसंबंध की अनुपस्थिति को माप सकता है।

प्र.13. एक सप्ताह तक अपने स्थानीय बाजार से 5 प्रकार की सब्जियों की कीमतें प्रतिदिन एकत्र करें। उनका सहसंबंध गुणांक परिकलित कीजिए। इसके परिणाम की व्याख्या कीजिए।
उत्तर :
इसका उत्तर छात्र प्रति छात्र भिन्न होगा। परंतु विधि इस प्रकार होगी।

प्र.14. अपनी कक्षा के सहपाठियों के कद मापिए। उनसे उनके बेंच पर बैठे सहपाठी का कद पूछिए। इन दो चरों का सहसंबंध गुणांक परिकलित कीजिए और परिणाम का निर्वचन कीजिए।
उत्तर :
सभी बेंचों पर दायीं ओर बैठे छात्र को X तथा बायीं और बैठे छात्र की Y कहें। यदि कक्षा में 40 विद्यार्थी हैं तो 20 जोड़े बन जायेंगे। यदि संख्या विषम है तो एक विद्यार्थी को छोड़ना होगा। उनके कद ज्ञात करके कार्ल पियरसन की किसी भी विधि द्वारा सहसंबंध गुणांक ज्ञात किया जा सकता है।

प्र.15. कुछ ऐसे चरों की सूची बनाएँ जिनका परिशुद्ध माप कठिन हो।
उत्तर :
ऐसे कुछ चर इस प्रकार हैं:

(क) सुंदरता
(ख) बुद्धिमत्ता
(ग) ईमानदार
(घ) अनुशासन
(ङ) आत्मविश्वास
(च) संस्कार

प्र.16. r के विभिन्न मानों +1, -1, तथा 0 की व्याख्या करें।
उत्तर :
r = +1 पूर्ण धनात्मक सहसंबंध
r = -1 पूर्ण ऋणात्मक सहसंबंध
r = 0 रेखीय सहसंबंध की अनुपस्थिति।

प्र.17. पियरसन सहसंबंध गुणांक से कोटि सहसंबंध गुणांक क्यों भिन्न होता है?
उत्तर :
पियरसन सहसंबंध गुणांक की भाँति श्रेणी सहसंबंध भी + 1 तथा – 1 के बीच स्थित होता है। हालाँकि, सामान्य तौर पर यह सामान्य विधि की तरह यथावत नहीं होता है। इसका कारण यह है कि इसमें आँकड़ों से संबंधित सभी सूचनाओं का उपयोग नहीं होता है। श्रृंखला में मदों के मानों के वे प्रथम अंतर जो उनके परिमाण के अनुसार क्रम में व्यवस्थित किए जाते हैं, आमतौर पर कभी स्थिर नहीं होते। सामान्यतः आँकड़ा-कुछ केंद्रीय मानों के आसपास सारणी के मध्य में थोड़े बहुत अंतर पर एकत्रित होते हैं। यदि समान अंत्र पर स्थिर होते, तब r और rk समान परिमाण देते। प्रथम अतंर तथा क्रमिक मानों में अंतर होता है। कोटि सहसंबंध को पियरसन गुणांक की अपेक्षा तब अधिक प्राथमिकता दी जाती है, जब चरम मान दिए गए हों। सामान्यतः rk का मान r से कम या इसके बराबर होता है।

प्र.18. पिताओं (x) और उनके पुत्रों (y) के कदो का माप नीचे इंचों में दिया गया है। इन दोनों के बीच सहसंबंध गुणांक परिकलित कीजिए।

उत्तर :

प्र.19. x और y के बीच सहसंबंध गुणांक को परिकलित कीजिए और उनके संबंध पर टिप्पणी कीजिए।

उत्तर :

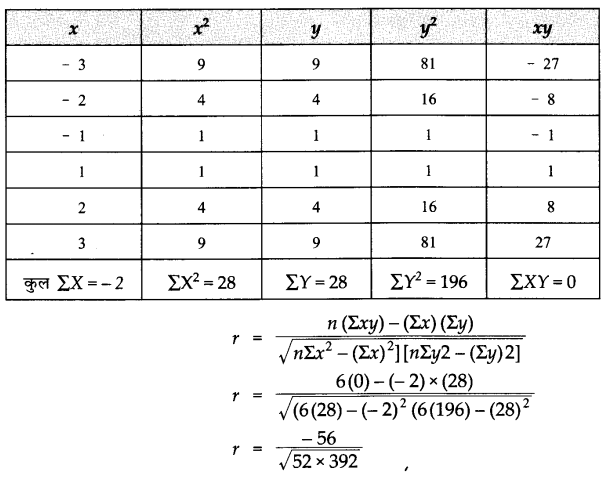
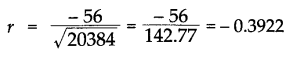
प्र.20. x और y के बीच सहसंबंध गुणांक परिकलित कीजिए और उनके संबंध पर टिप्पणी कीजिए।

उत्तर :

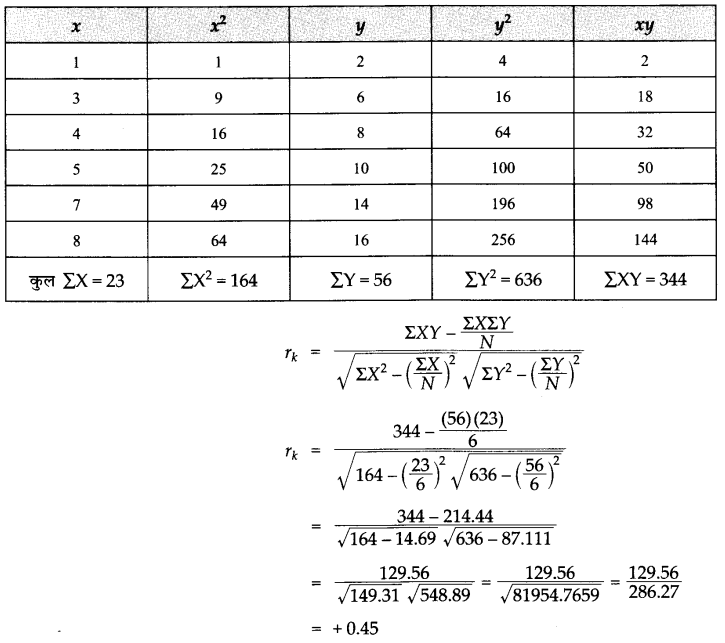
NCERT Class 11 Arthshastra अर्थशास्त्र में सांख्यिकी (Sankhyiki)

Class 11 Arthshastra Chapters | Arthshastra Class 11 Chapter 7

NCERT Solutions for Class 11 Economics (Hindi Medium)

NCERT Solutions for Class 11 Economics (Hindi Medium): Statistics for Economics (खण्ड-1 अर्थशास्त्र में सांख्यिकी)

NCERT Solutions For Class 11 Arthshastra Chapter 1 परिचय
NCERT Solutions For Class 11 Arthshastra Chapter 2 आँकड़ों का संग्रह
NCERT Solutions For Class 11 Arthshastra Chapter 3 आँकड़ों का संगठन
NCERT Solutions For Class 11 Arthshastra Chapter 4 आँकड़ों का प्रस्तुतीकरण
NCERT Solutions For Class 11 Arthshastra Chapter 5 केंद्रीय प्रवृत्ति की माप
NCERT Solutions For Class 11 Arthshastra Chapter 6 परिक्षेपण के माप
NCERT Solutions For Class 11 Arthshastra Chapter 7 सहसंबंध
NCERT Solutions For Class 11 Arthshastra Chapter 8 सूचकांक
NCERT Solutions For Class 11 Arthshastra Chapter 9 सांख्यिकीय विधियों के उपयोग

NCERT Solutions for Class 11 Economics (Hindi Medium)

NCERT Solutions for Class 11 Economics: Indian Economic Development (खण्ड -2 भारतीय अर्थव्यवस्था का विकास)

NCERT Solutions For Class 11 Arthshastra Chapter 1 स्वतंत्रता की पूर्व संध्या पर भारतीय अर्थव्यवस्था
NCERT Solutions For Class 11 Arthshastra Chapter 2 भारतीय अर्थव्यवस्था (1950-1990)
NCERT Solutions For Class 11 Arthshastra Chapter 3 उदारीकरण, निजीकरण और वैश्वीकरण-एक समीक्षा
NCERT Solutions For Class 11 Arthshastra Chapter 4 निर्धनता
NCERT Solutions For Class 11 Arthshastra Chapter 5 भारत में मानव पूँजी का निर्माण
NCERT Solutions For Class 11 Arthshastra Chapter 6 ग्रामीण विकास
NCERT Solutions For Class 11 Arthshastra Chapter 7 रोजगार-संवृद्धि, अनौपचारीकरण एवं अन्य मुद्दे
NCERT Solutions For Class 11 Arthshastra Chapter 8 आधारिक संरचना
NCERT Solutions For Class 11 Arthshastra Chapter 9 पर्यावरण और धारणीय विकास
NCERT Solutions For Class 11 Arthshastra Chapter 10 भारत और इसके पड़ोसी देशों के तुलनात्मक विकास अनुभव

NCERT Solutions for Class 12 All Subjects	NCERT Solutions for Class 10 All Subjects
NCERT Solutions for Class 11 All Subjects	NCERT Solutions for Class 9 All Subjects

NCERT SOLUTIONS